自由落下する物体の速度を求めることは、物理学の基本的なスキルであり、様々な実用的な場面で必要とされます。落下速度を正確に計算できることは、安全設計や実験計画において非常に重要です。
本記事では、自由落下の速度の求め方と公式を詳しく解説し、終端速度や最高速度の概念についても説明していきます。グラフを使った理解や具体的な計算方法まで幅広くご紹介しましょう。
それでは、自由落下の速度について順を追って見ていきましょう。
速度を求める基本公式
それではまず速度を求める基本公式について解説していきます。
2つの基本公式
自由落下の速度を求めるには、主に2つの公式があります。時間がわかっている場合と距離がわかっている場合で使い分けるのです。
【速度を求める2つの基本公式】
① 時間から速度:v = gt
② 距離から速度:v = √(2gh)
(v:速度、g:重力加速度、t:時間、h:距離)
公式①は速度が時間に比例することを示しており、公式②は速度と距離の関係を表しています。どちらも等加速度運動の一般式から導出できるでしょう。
公式の導出
これらの公式は、等加速度運動の公式 v = v₀ + at と v² = v₀² + 2ax に、自由落下の条件(初速度v₀ = 0、加速度a = g)を適用することで得られます。
v = v₀ + at に v₀ = 0、a = g を代入すると、v = gt となります。
v² = v₀² + 2ax に v₀ = 0、a = g、x = h を代入すると、v² = 2gh となり、両辺の平方根をとって v = √(2gh) が得られるのです。
公式の使い分け
問題によって与えられる情報が異なるため、適切な公式を選択することが重要です。何がわかっていて何を求めたいのかを明確にしましょう。
| 与えられている情報 | 使用する公式 | 計算の特徴 |
|---|---|---|
| 落下時間 | v = gt | 掛け算だけで簡単 |
| 落下距離(高さ) | v = √(2gh) | 平方根の計算が必要 |
| 時間と距離の両方 | どちらでもOK | 検算に使える |
時間から速度を求める方法
続いては時間から速度を求める方法を確認していきます。
基本的な計算
落下時間がわかっているときの速度は、v = gt という最も基本的な公式で求められます。重力加速度gに時間tをかけるだけの簡単な計算です。
【計算例1】物体を自由落下させて4秒後の速度を求めよ。(g = 10 m/s²とする)
【解答】
v = gt = 10 × 4 = 40 m/s
答え:40 m/s
この計算から、1秒ごとに10 m/sずつ速度が増加していくことがわかります。時間が2倍になれば速度も2倍になるという比例関係です。
異なる時刻での速度
様々な時刻での速度を計算すると、速度の増加の様子が明確になります。この関係を理解することで、速度の変化を直感的に把握できるでしょう。
| 時間(秒) | 速度(m/s) | 増加量(m/s) |
|---|---|---|
| 0 | 0 | – |
| 1 | 10 | 10 |
| 2 | 20 | 10 |
| 3 | 30 | 10 |
| 4 | 40 | 10 |
表からわかるように、毎秒10 m/sずつ一定の割合で速度が増加しています。これが等加速度運動の特徴なのです。
g = 9.8 m/s²を使った計算
より正確な計算が必要な場合は、g = 9.8 m/s²を使用します。計算結果が小数になることが多いでしょう。
【計算例2】3秒間自由落下した物体の速度を求めよ。(g = 9.8 m/s²とする)
【解答】
v = gt = 9.8 × 3 = 29.4 m/s
答え:29.4 m/s
g = 10 m/s²を使った場合の答え(30 m/s)と比べると、約2%の差があります。精密な計算が求められる場合は、g = 9.8 m/s²を使うべきです。
距離から速度を求める方法
続いては距離から速度を求める方法を確認していきます。
平方根を使った計算
落下距離がわかっているときは、v = √(2gh) を使用します。時間を経由せずに直接速度が求められるため便利です。
【計算例3】高さ45mから物体を自由落下させた。地面到達直前の速度を求めよ。(g = 10 m/s²とする)
【解答】
v = √(2gh) = √(2 × 10 × 45)
= √900 = 30 m/s
答え:30 m/s
計算の手順としては、まず2ghを計算してから平方根をとります。多くの場合、きれいな数値になるように問題が作られているでしょう。
様々な高さでの速度
異なる高さから落下した場合の速度を比較すると、距離と速度の関係が明確になります。
| 高さ(m) | 2gh | 速度(m/s) |
|---|---|---|
| 5 | 100 | 10 |
| 20 | 400 | 20 |
| 45 | 900 | 30 |
| 80 | 1600 | 40 |
| 125 | 2500 | 50 |
高さが4倍になると速度は2倍になることがわかります。これは速度が距離の平方根に比例するという関係を示しているのです。
エネルギー保存則による導出
速度の公式 v = √(2gh) は、エネルギー保存則からも導出できます。位置エネルギーmghが運動エネルギー(1/2)mv²に変換されるという考え方です。
【エネルギー保存則による導出】
位置エネルギー = 運動エネルギー
mgh = (1/2)mv²
両辺をmで割る:gh = (1/2)v²
両辺を2倍:2gh = v²
平方根をとる:v = √(2gh)
このように、運動方程式を使った導出とエネルギー保存則を使った導出の両方で同じ結果が得られます。物理学の美しさの一つでしょう。
速度のグラフと特徴
続いては速度のグラフと特徴を確認していきます。
速度-時間グラフ(v-tグラフ)
自由落下のv-tグラフは、原点を通る直線となります。速度v = gtが時間tに比例するためです。
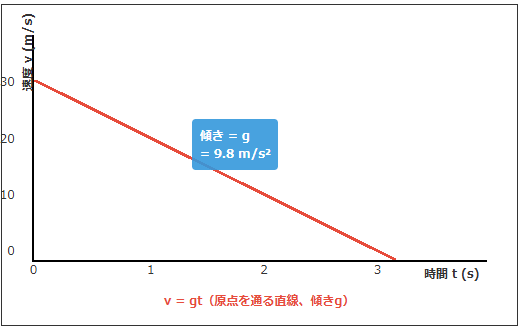
このグラフの傾きは重力加速度gであり、時間が経つほど速度が直線的に増加していくことを示しています。
速度-距離グラフ
速度と距離の関係 v = √(2gh) をグラフにすると、平方根の形の曲線となります。距離が増加するにつれて速度も増加するが、増加率は徐々に小さくなるのです。
このグラフから、同じ距離を進んでも、最初の方が速度の増加が大きいことがわかります。
グラフからの情報読み取り
v-tグラフからは様々な情報を読み取ることができます。グラフを活用することで、計算を簡略化できる場合もあるでしょう。
【v-tグラフから読み取れる情報】
・グラフの傾き → 加速度(g)
・グラフの面積 → 移動距離
・特定時刻の高さ → その時点の速度
・2点間の傾き → 平均加速度(常にg)
終端速度と限界速度
続いては終端速度と限界速度を確認していきます。
終端速度とは
終端速度とは、空気抵抗がある場合に物体が到達する最大の速度のことです。理想的な自由落下では速度は無限に増加し続けますが、実際には空気抵抗によって限界があります。
終端速度では、重力と空気抵抗がつりあい、それ以上加速しなくなるのです。速度が一定となり、等速直線運動に移行します。
スカイダイバーの終端速度は、腹這い姿勢で約55 m/s(時速約200km)、頭から突っ込む姿勢では約90 m/s(時速約320km)となります。
終端速度の計算
空気抵抗が速度に比例する場合(F = kv)、終端速度v∞は重力と空気抵抗がつりあう条件 mg = kv∞ から、v∞ = mg/k と求められます。
【終端速度の例】
質量0.5kg、抵抗係数k = 0.5 N·s/mの物体
v∞ = mg/k = (0.5 × 10) / 0.5 = 10 m/s
終端速度は質量に比例し、抵抗係数に反比例します。重い物体ほど、また抵抗を受けにくい形状ほど、終端速度は大きくなるでしょう。
空気抵抗がある場合の速度変化
空気抵抗がある場合、速度は時間とともに終端速度に漸近していきます。最初は急激に増加しますが、徐々に増加率が小さくなるのです。
| 物体 | 終端速度(概算) |
|---|---|
| 雨粒(直径1mm) | 約4 m/s |
| 雨粒(直径5mm) | 約9 m/s |
| スカイダイバー(腹這い) | 約55 m/s |
| パラシュート展開後 | 約5 m/s |
まとめ
自由落下の速度は、時間がわかっている場合は v = gt、距離がわかっている場合は v = √(2gh) で求められます。速度は時間に比例し、距離の平方根に比例するという関係があります。
v-tグラフは原点を通る直線となり、その傾きは重力加速度gです。実際の落下では空気抵抗により終端速度が存在し、それ以上は加速しなくなります。終端速度は物体の質量、形状、空気抵抗係数によって決まるのです。
速度の計算方法を理解することで、落下現象の予測や安全設計に応用でき、物理学の実用的なスキルとして役立つでしょう。


の単位変換・換算方法は?例題付きで解説!【1atmは何mmhg?1mmhgは何atm】-1-320x180.png)
